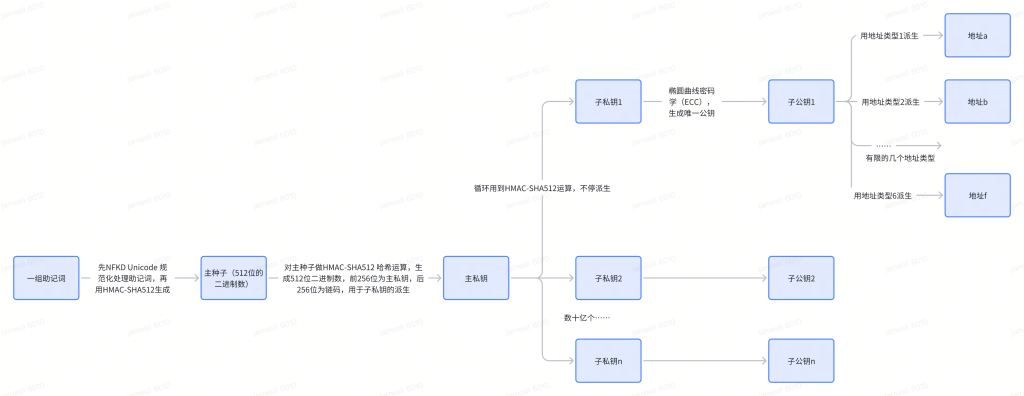
• 助记词：通常由12-24个单词组成。这些单词是从2048个预定义单词中随机选择的。助记词可能的组合数：
  • 对于12个单词的助记词：2048^12 ≈ 5.44 × 10^39 种可能性。
  • 对于24个单词的助记词：2048^24 ≈ 2.96 × 10^79 种可能性。
• 私钥：由助记词经过一系列的哈希过程生成的主私钥，主私钥经过派生成子私钥
• 公钥：由私钥生成，用于验证签名和生成地址。
• 地址：用于接收比特币的标识符。地址是公钥的哈希值，提供了额外的安全层。比特币链上记录的是地址，而不是公钥。使用地址收币，公钥不暴露。使用地址法币，公钥暴露。

在UTXO模型中，每次转账，剩余的零钱会进入到一个新的地址，这个地址也就对应另外一组私钥和公钥。

Q：穷举所有助记词，并查看钱包中有没有钱是否可行？

A：不可行。即使使用世界上最强大的超级计算机，也需要比宇宙年龄还要长得多的时间来穷举。具体的计算过程：

1. 以12个单词的助记词组合总数为例:

2048^12 ≈ 5.44 × 10^39

2. 假设使用世界上最快的超级计算机:

以 2022 年的 Frontier 超级计算机为例,其峰值性能为 1.1 exaflops (1.1 × 10^18 次浮点运算/秒)

3. 假设每次尝试一组助记词需要 100 次浮点运算 (这是一个保守估计,实际可能更多):

每秒可尝试的组合数 = 1.1 × 10^18 / 100 = 1.1 × 10^16

4. 穷举所有组合所需时间:

5.44 × 10^39 / (1.1 × 10^16) ≈ 4.95 × 10^23 秒

5. 转换为年:

4.95 × 10^23 秒 / (365 * 24 * 3600) ≈ 1.57 × 10^16 年

6. 比较:

宇宙年龄约为 13.8 × 10^9 年

穷举时间是宇宙年龄的约 1,138,405 倍

对于单组助记词的处理时间:

1. 生成一组助记词的时间:

– 通常在毫秒级别,假设 1ms

2. 检查钱包是否有余额:

– 这涉及网络请求,可能需要 100ms 到几秒不等

– 假设平均 500ms

3. 总时间:

1ms + 500ms = 501ms ≈ 0.5 秒

但要注意:

– 网络延迟可能大幅增加检查时间

– 区块链的响应时间也会影响

– 批量处理可能会提高效率

即使我们能够每秒检查 2 个地址(这是非常乐观的估计),穷举所有可能性仍需要:

5.44 × 10^39 / 2 ≈ 2.72 × 10^39 秒 ≈ 8.62 × 10^31 年

这个时间跨度远远超出了宇宙的预期寿命。

总结:

虽然检查单个助记词组合的时间相对较短,但由于可能的组合数量巨大,完全穷举在计算上是不可行的。这就是为什么比特币等加密货币被认为是安全的 – 它们的安全性建立在这种数学上的不可行性之上。