什么是二叉树?
在计算机科学中,二叉树(binary tree)是每个节点最多只有两个分支的树结构。
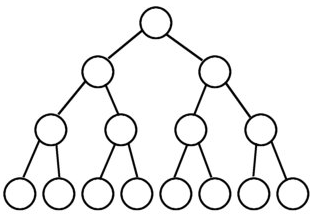
如上图的 二叉树,第 i 层至多拥有 \(2^{i-1}\) 个节点 。
这样的二叉树,节点数增加速度呈现指数增长,后面增长速度非常快。
股价二叉树
定义
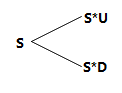
在研究期权定价中,我们构造的股价二叉树,为了让节点增长速度增长可控,我们让股价每次上涨下跌的幅度保持不变,所以可以选择下图的模型。
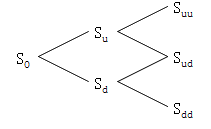
如上图的 二叉树,第 i 层至多拥有 i 个节点 。
binomial option pricing model 三个特点:
- 起始的资产价格是 \(S_{0}\)
- 上涨下跌的幅度分别是 U 和 D
- 上涨下跌的概率分别是 \(\pi _{U}\) 和 \(\pi _{D}\)
CFA 考试中通常会告诉 U 和 D 分别是多少。
如果考试中只告诉了 U 和 D 其中之一,另一个就取倒数(\(U =\frac{1}{D}\))
为什么不选择三叉树?
我们不选择三叉树主要是考虑到计算机的算力,对计算机的处理能力要求很高。我们每一次分叉是经历 t 时长分成两个分支,我们要提高精度只需要让 \(t \to 0\) 一样能实现。
利率二叉树 & 股价二叉树
股价二叉树是源于利率二叉树。利率二叉树源于塔克曼的 Model 1:\(dr=\sigma dw\)
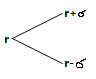
利率是一个率的概念,转换成股价,我们对股价取 ln 得到股票的回报率。
这里是基于股价服从对数正态分布,那么 “ln 股价” 就服从正态分布。
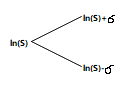
这里对每一项加上 e 底数得到股价二叉树模型。
风险中性下的上涨下跌概率
公式
$$\pi_{U} = \frac{(1 + r_{f})^{T} – D}{U – D}$$
$$\pi_{D} = 1 – \pi_{U} = \frac{U – (1 + r_{f})^{T}}{U – D}$$
推导过程

如上图,股价经过 t 时间分叉,上涨概率是\(\pi_{U}\),下跌概率是 \(1-\pi_{U}\)。
那么 t 时刻股价的期望是:
$$E(S_{t}) = \pi_{U} \times(S_{0}*U) + (1-\pi_{U})\times (S_{0}*D)$$
风险中性下,投资者多承担风险不会得到额外的回报,所有投资者的预期收益都是 risk free rate。 所以站在 0 时刻去看 t 时刻远期的股价期望:
$$E(S_{t}) = S_{0}(1+r_{f})^{t}$$
联立上面两个式子即可得到风险中性下的上涨下跌概率。
tips:风险中性下的上涨下跌概率更像是长得像概率的系数。
Binomial Option Pricing Model 二叉树期权定价模型
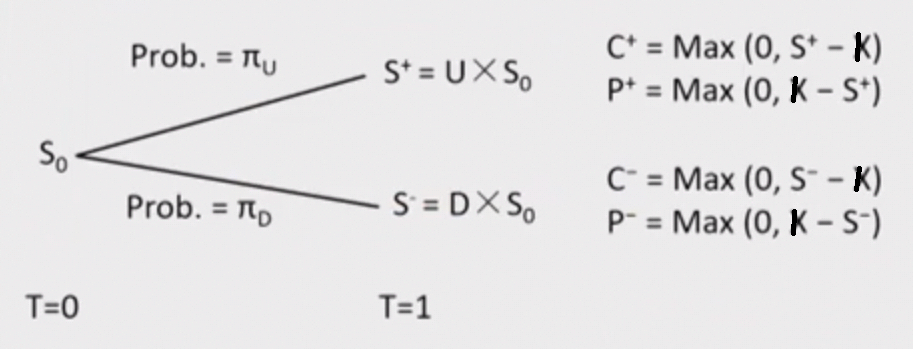
通过一个分叉阶段的股价二叉树,我们可以得到 T 时刻的 call 和 put 的价格(即内在价值,到期不存在时间价值),再用无风险利率向前折现到 0 时刻即可得到 0 时刻的看涨期权和看跌期权的价值。
Value of an call option
$$C_{0} = (\pi_{U} \times C^{+} + \pi_{D} \times C^{-})/(1+r_{f})^{T}$$
Value of an put option
$$P_{0} = (\pi_{U} \times P^{+} + \pi_{D} \times P^{-})/(1+r_{f})^{T}$$
tips:如果这里是无股利支付的欧式期权,有了 call 的价格,用 put call parity 去计算 put 的价格也是可以的。详见:
Delta 对冲
Risk Free Hedge
如果我 short 一份 call,同时 long \(\delta \) 份的股票,进行无风险对冲。当前的投资组合现值是:
$$ V = \delta\times S -C $$
经过一个阶段分叉之后得到:
$$ V^{+} = \delta\times S^{+} -C^{+} $$
$$ V^{-} = \delta\times S^{-} -C^{-} $$
由于选定的 \(\delta\) 使得这一投资组合是无风险的,也就是无论股价上涨还是下跌,投资组合的价值是变的,即 \(V^{+} = V^{-}\)。于是,由上述两式可得:
$$\delta= \frac{C^{+} – C^{-}}{S^{+} – S^{-}} = \frac{C^{+} – C^{-}}{S \times U – S \times D}$$
tips:由于\(\delta\) < 1,所以 delta 对冲中,股票的份数一定是少于期权的份数的。
Arbitrage Oppotunity 套利机会
如果发现期权的市场价格(market price)与二叉树模型计算的(自己认为的)价值(calculated value)不相等,就存在套利机会。
如果 market price > calculated value,可以:
- short 1份 call,long \( \delta \) 份的股票
- 或者 short 1份 put,short \( \delta \) 份的股票
如果 market price < calculated value,可以:
- long 1份 call,short \( \delta \) 份的股票
- long 1份 put,long \( \delta \) 份的股票
发表评论