Fixed Income Futures 在 CFA 中指的就是国债期货。这一工具主要是用来管理利率风险的,如果用公司债期货的话会引入信用风险,所以一般用国债期货。
Fixed Income 知识回顾
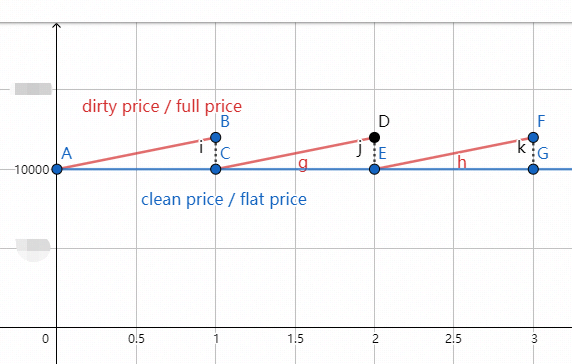
债券的报价是不含 应计利息 accrued interest(AI) 的,也就是 flat price 或者 clean price。而含有 AI 的价格叫 full price 或者 dirty price。
- clean price / flat price(不含AI)
- dirty price / full price (含AI)
债券的交易是以 full price 进行交易的,而债券的报价是以 flat price 进行报价的。
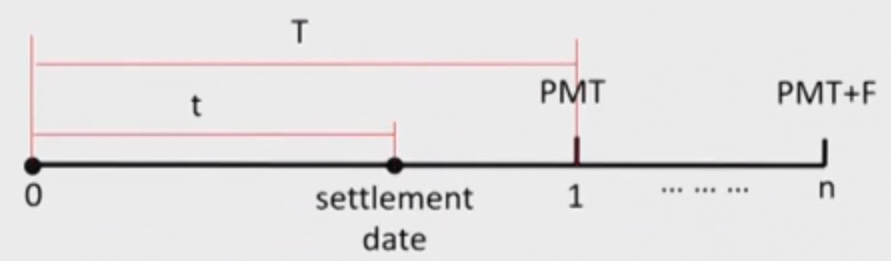
如图所示,债券在 settlement date 发生交易,在 1 时刻付息。买卖双方在交易的时候,买方肯定要对卖方在 t 期间持有债券的行为给与补偿,也就是说交易价格要包含 accrued interest。
$$AI = \frac{t}{T}\times PMT$$
而报价的时候为了价格的平滑,所以用不包含 AI 的 flat price。
on-the-run:指距离现在最近一次发行的国债
off-the-run:指除了最近一次以外的以前发行的国债
Fixed Income Futures
国债期货合约在实物交割的时候,空方可以选择不止一种券交割给多方。
美国的国债期货市场上,国债期货合约在签订的时候,就约定了可供选择交割的一篮子券,要求面值是 $100000 的任何 coupon rate 的 T-bonds 长期国债,长期债券不短于 15 年。其中 T-bonds 的报价是以 32 分位来进行报价的,例如:一个报价为 “95-18”,这代表 95+18/32=95.5625 元
为什么是空头来决定交割哪个券?
- 现实中:国债一般是滚动发行的,同一时刻市场上有很多批次的国债(它们的 coupon rate 可能不同,不同时刻发行的国债市场状况都不同)
- 防止(多)逼空。某一只国库券 A 在二级市场的流动性未必很好。如果临近交割时,多方与其利益一致方一起,提前大量收走市面上流通的国库券 A,就容易出现逼空的现象,空方一时就买不到,无券可交。为了稳定国债市场,防止这种多逼空的现象出现,国债期货在签订的时候就允许交割一篮子国债,并把选择权给空方。
国债期货的底层标的是什么?
国债期货的 Underlying Asset 是一个假想的 coupon rate 为 6% 的 30 年期国债,它是用于报价的。而实际交割的时候还是从 A basket of deliverable bonds 里面的券去交割。
虚拟债券的报价怎么指导实际债券交易呢?这里要引入一个转换因子(CF)。
转换因子 Conversion factor(CF)
转换因子(CF)是用于把国债期货报价(基于虚拟债券)和实际交割券的价格连接起来。可交割的一篮子债券中,每只债券都会给一个对应的 CF,是交易所提供的,目的是让可交割的债券价格大致相等 。
实际交割券的价格 = 国债期货报价(QFP) x CF + AI
$$ Principal invoice amount = Quoted futures price \times CF $$
$$Total invoice amount = Principal invoice amount + accrued interest $$
这里,Principal invoice amount 是不含应计利息的 clean price 。
国债期货的交割过程
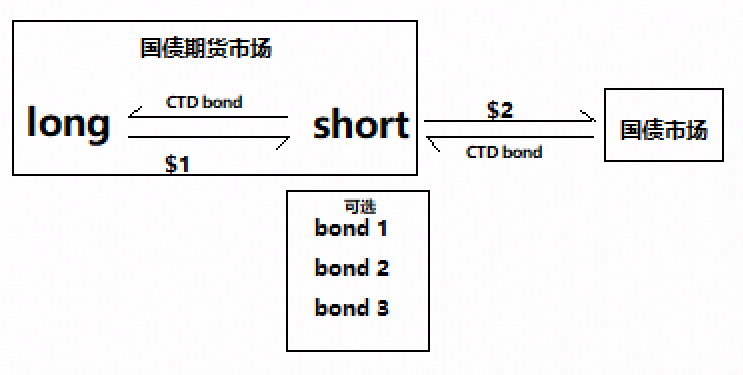
如上图所示,国债期货到期时,short 方有权利在一篮子债券中挑选一个成本最低是债券,从国债市场花 $2 买来,然后交割给 long 方,同时收取 $1。
这里要引入一个 CTD(cheapest-to-deliver) 的概念。
CTD Bond(cheapest-to-deliver)
a cheapest-to-deliver(CTD) bond 是指国债期货可供交割的一篮子券当中,考虑到 CF 之后,成本最低的一只债券。
$2 是 short 方从市场上买来债券花的钱,所以:
$2 = CTD bond clean price + AI
$1 是 short 方从 long 方手里收来的钱,所以:
$1 = QFP x CF + AI
由于 short 方从国债市场上买来 CTD bond,和把 CTD bond 交割给 long 方是在同一时间,所以上面两个式子中的 AI 是一样的。
所以, short 方的交割成本 = $2 – $1 = CTD bond clean price – QFP x CF
Pricing of Fixed Income Futures 国债期货定价
$$Quoted Futures Price = [(S_{0} – PVC) \times (1+r_{f})^{T} – AI_{T}]/CF$$
- \(S_{0}\):真实的国债(T-bond )的即期 dirty price
- \(S_{0} = quoted price (T-bond’s clean price) + AI_{0}\)
- PVC:国债期货存续期间(0 – T),交割的真实债券的期间流入票息的现值
- \(AI_{T}\):交割日距离之前最近一次付息日,期间累积的应计利息
其中,\((S_{0} – PVC) \times (1+r_{f})^{T}\) 是从现券的角度,通过要交割的这只债券的现价(dirty price)计算未来 T 时刻交割的价值。
上式中,用每一组债券的 \(S_{0}\) 和 CF 和 PVC,都可以计算 QFP。由于计算结果差不多,所以选一组计算即可。
\(AI_{0}\) 和 \(AI_{T}\)是什么关系?
\(AI_{0}\) 是站在 0 时刻,要交割的现券距离当前最近的一次派发票息的时刻到现在,累积的应计利息。
\(AI_{T}\) 是站在未来交割的时刻 T,要交割的现券距离 T 最近的一次派发票息的时刻到 T 时刻,累积的应计利息。
发表评论