远期利率&即期利率

即期利率是从现在开始到未来某个时间点，期间的年化利率。比如：一年期的即期利率，两年期的即期利率……

远期利率是从未来的某个时间点到另一个时间点的利率水平 。确定了收益率曲线后，所有的远期利率都可以根据收益率曲线上的即期利率求得，远期利率是和收益率曲线紧密相连的。

FRA 定义

远期利率协议（forward rate agreement）是一个场外的远期合约，其底层标的是浮动利率（e.g. Libor）。

Long Positon 是未来有义务以约定利率借入钱的一方（受益于标的资产价格上涨。到期的实际利率越高，说明 forward 签对了！）

术语：long position borrow at the fixed rate, floating receiver（这里是一个固定说法。到期之后如果是现金交割的话， short 方要给到 long 方补偿，补偿的借贷利率是：实际利率 – FR。FR 是固定的，所以 实际利率-FR 是浮动利率）。

Short Position 是未来有义务以约定利率贷出钱的一方 （受益于标的资产价格下跌。到期的实际利率越低，说明 forward 签对了！）

术语：short position lend at the fixed rate, fixed receiver。

FRA 形式

The notation of FRA is typically “\(a\times b\) FRA “

a：the number of months until the contract expires

b：the number of months until the underlying loan is settled

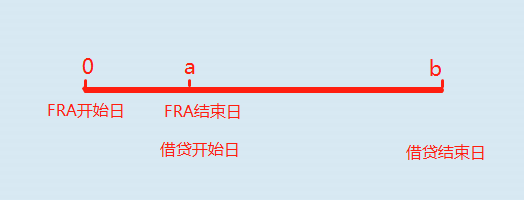
由上图可知，FRA 持续时间是 a，借贷持续时间是 b – a。

这里插一个例子： swaption 互换期权 ，这个衍生品让 long 方将来有权利进入到一个 swap 合约当中。那么 0 时刻对应的就是 option 开始日，a时刻既是option结束日，又是 swap 开始日（如果行权的话），b时刻是 swap 结束日

FRA的用途

锁定利率，对冲未来借入或者贷出利率的风险。

假设FRA 到期时选择现金交割，如果 FRA rate < spot rate，long 方会收到补偿。如果 FRA rate > spot rate，short 方会收到补偿。

$$补偿 = NP \times 利差 \times 借贷时间$$

NP：名义本金（notional principal）

注：FRA 中是不考虑复利的，用单利（\(1+r\times n\)）。

FRA 的定价

FRA rate 是通过一系列的即期利率计算的，并且是单利模式。

定价公式：

$$1+ S_{0}(b) \times \frac{b}{12} = (1+ S_{0}(a) \times \frac{a}{12})\times (1+FR_{0}\times \frac{b-a}{12})$$

\(S_{0}(a)\) 和 \(S_{0}(b)\) 是站在 0 时刻看0 – a 期间和 0 – b 期间的即期利率，这个是在市场上有定价的。而 \(FR_{0}\) 是站在 0 时刻看待 a 到 b 这段时间的远期利率，是我们要计算的。

由上式算出 \(FR_{0}\)。

FRA 的估值

首先，我们要确定，0 时刻、t 时刻 、 T 时刻分别在哪里。

FRA 在 0 时刻的价值

$$V_{L} = V_{S} = 0$$

FRA 在 T 时刻的价值

FRA 虽然在 a 时刻就结束了，但是利息是在 b 时刻支付的。所以如果要计算 a 时刻的价值，应该把 b 时刻发生的付息向前折现到 a 时刻。实际 FRA 结算的时间是在 a 时刻。

在 T 时刻，

对 long position 来说，\( 利差 = S_{T}(b) – F_{0}(T) \)。

对 short position 来说，\(利差 = F_{0}(T) – S_{T}(b)\)。

其中，\( S_{T}(b) \) 是 T 时刻看 a – b 期间的即期利率。 \(F_{0}(T)\) 是 0 时刻在 FRA 上签订的价格。

所以，T 时刻对于 long position 的价值应该是：

$$ V_{L,T} = \frac{NP\times ( S_{T}(b) – F_{0}(T) )\times \frac{Days}{360}}{1+ S_{T}(b) \times \frac{Days}{360}}$$

其中，Days 就是借贷期间的天数，也就是（b – a）。

FRA 在 t 时刻的价值

那么如何计算 t 时刻的价值呢？这里要分两个步骤。

计算 t 时刻的新的 \(FR_{t}\)

在 t 时刻重新签订一份\((a-t) \times b\) FRA

$$(1+S_{t}(b))^{b-t} = (1+S_{t}(a))^{a-t}\times (1+FR_{t})^{b-a}$$

其中，\( S_{t}(b)\)是在 t 时刻看 t – b 期间的即期年化利率。 \( S_{t}(a)\)是在 t 时刻看 t – a 期间的即期年化利率，这两个利率都是市场上有的。

\( FR_{t}\)是在 t 时刻看 a – b 期间的远期利率（ 年化 ）。

通过上式把 t 时刻的 a – b 期间的借贷利率 \( FR_{t}\) 算出来。

计算 t 时刻 long position 的价值

$$V_{L,t} = \frac{NP \times (FR_{t}-F_{0}(T))\times \frac{b-a}{360}}{1+S_{b-t}\times \frac{b-t}{360}}$$

注意：上式中分子的时间是借贷存续时间（b-a），而分母中的时间是 b 时刻的现金向 t 时刻进行折现。