Convex & Concave 凸&凹

首先要明确一个区分，Convex（凸）和 Concave（凹）。

Convex 是指二阶导数大于零的。

Concave，也叫 Negative Convex， 是指二阶导数小于零的。也可以通过下图做简单的记忆：

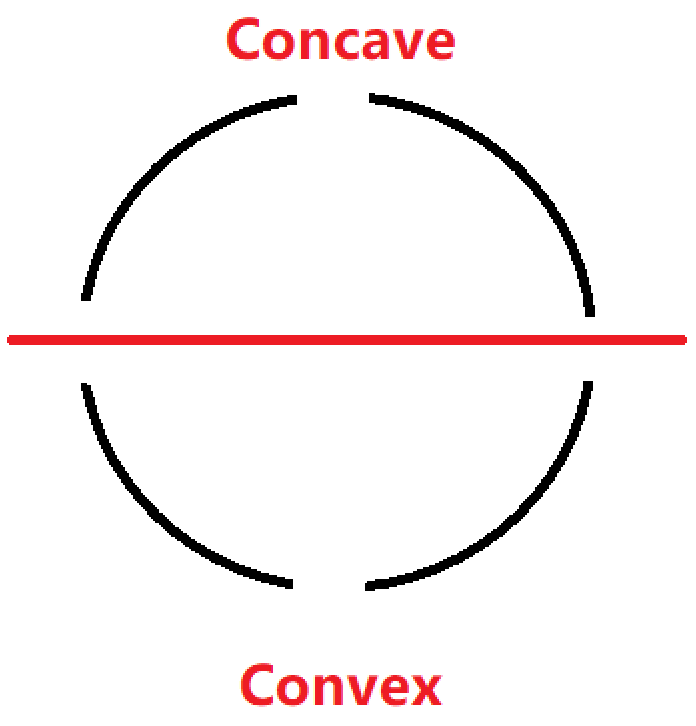
凸度的定义&应用

久期是当利率变动时，对债券价格进行线性估计。但是真实的债券价格-YTM图像是 Convex 的。那么，这条曲线越弯曲，用久期估算的误差就越大，就越迫切地需要用凸度来进行修正。

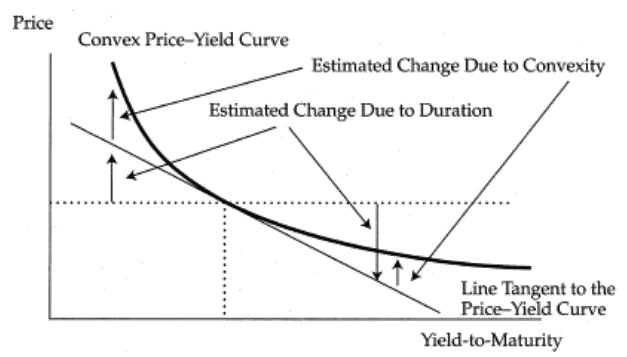
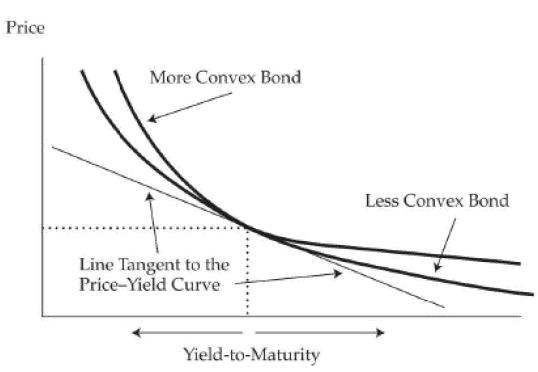
买凸度大的债券好还是买凸度小的债券好呢？

站在投资者的角度，买凸度大的债券是有利的。因为当利率上升，债券价格跌的少；当利率下降，债券价格涨的多。

久期&凸度计算公式

第一组是定义式，第二组是利率点变动，第三组是利率曲线变动。公式要记住。

在原有的修正久期对债券价格进行估计的公式基础上，我们引入凸度，对其进一步修正，让结果更接近，但是仍然是约等号，因为泰勒展开式后面有无穷项，这里只是引入了二阶项。

下式就是加上了凸度调整之后的公式，务必要记住：

$$ \frac{\Delta P}{P} \approx [- ModDur \times \Delta r] + [\frac{1}{2} \times Con \times (\Delta r)^{2}] $$

企业债券的 YTM 可以看成是一个政府债券 benchmark 收益率的基础上，加一个 spread 基差。这个基差与两个因素有关：一个是信用风险，一个是流动性风险。如果假设 benchmark 不变的话，上式可以变换成下式：

$$ \frac{\Delta P}{P} \approx [- ModDur \times \Delta Spread] + [\frac{1}{2} \times Con \times (\Delta Spread)^{2}] $$

Money duration & Money convexity

影响久期和凸度的因素

如果两个债券的久期是一样的，现金流分散程度越大，它的凸度越大。

所以，相同久期下，bullet bond 凸度小。

Callable Bond & Putable Bond

Callable Bond

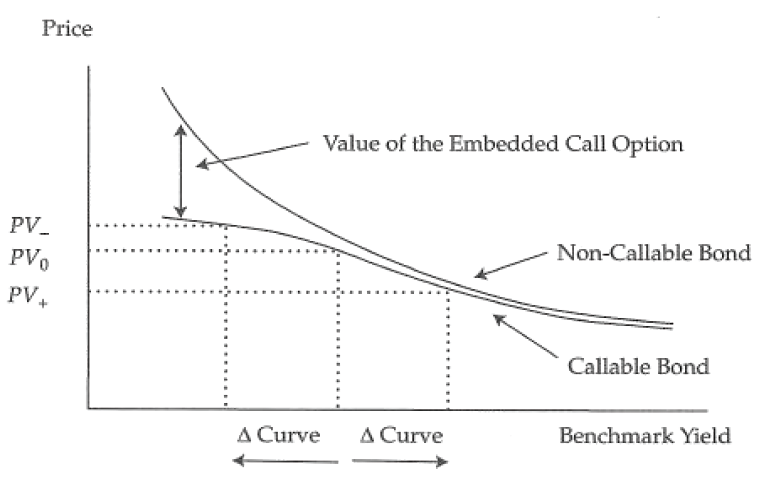
Callable Bond 有效久期比 普通债券更低。因为当利率比较低的时候，前者的 expected life 更短一点，呈现 negative convexity（concavity） 负凸性。

Putable Bond

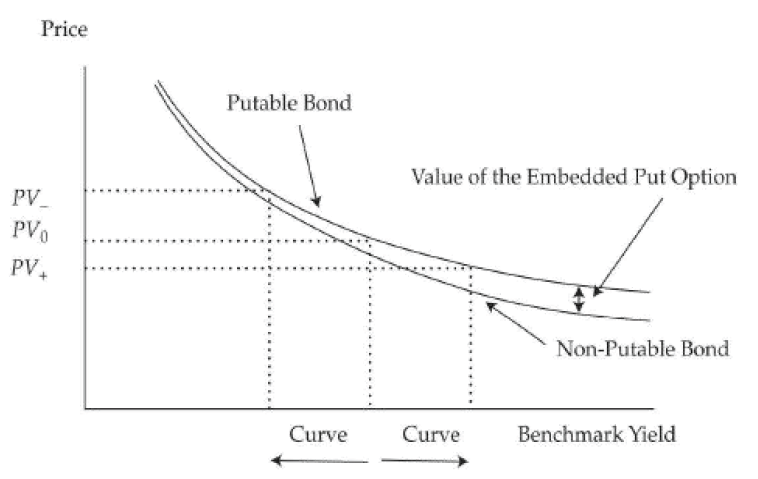
Putable Bond 有效久期比 普通债券更低。因为当利率比较高的时候，前者的 expected life 更短一点，呈现更高的凸性。