期权的价格与标的资产价格、标的资产波动率、期权执行价格、期权到期时间、利率等因素有关,通常用希腊字母(Greeks)表示期权价格对于上述影响因素变化的敏感程度,是期权交易中重要的风险管理指标。常用希腊字母及其含义如下表所示:
| 名称 | 符号 | 中文含义 | 数学表达式 (以 call 为例) |
| Delta | Δ | 标的资产价格变化引起期权价格变化的敏感度 | \(\frac{\Delta C}{\Delta S}\) |
| Gamma | γ | 标的资产价格变化引起 Delta 值变化的敏感度 | \(\frac{\Delta Delta}{\Delta S}\) |
| Theta | θ | 期权的时间价值随(已流逝)时间流逝耗损的速度 | \(\frac{\Delta C}{\Delta t}\) |
| Vega | ν | 隐含波动率变化引起的期权价格变化的敏感度 | \(\frac{\Delta C}{\Delta \sigma}\) |
| Rho | P | 无风险利率变化引起期权价格变化的敏感度 | \(\frac{\Delta C}{\Delta r_{f}^{c}}\) |
Delta 值
Delta,又称对冲值,表示期权价格对标的资产价格变化的敏感性,即标的资产价格变动一个单位时期权价格的变化率。
斜率
由 \(Delta = \frac{\Delta C}{\Delta S} \) 可知,Delta 就可以理解成下图中的斜率。
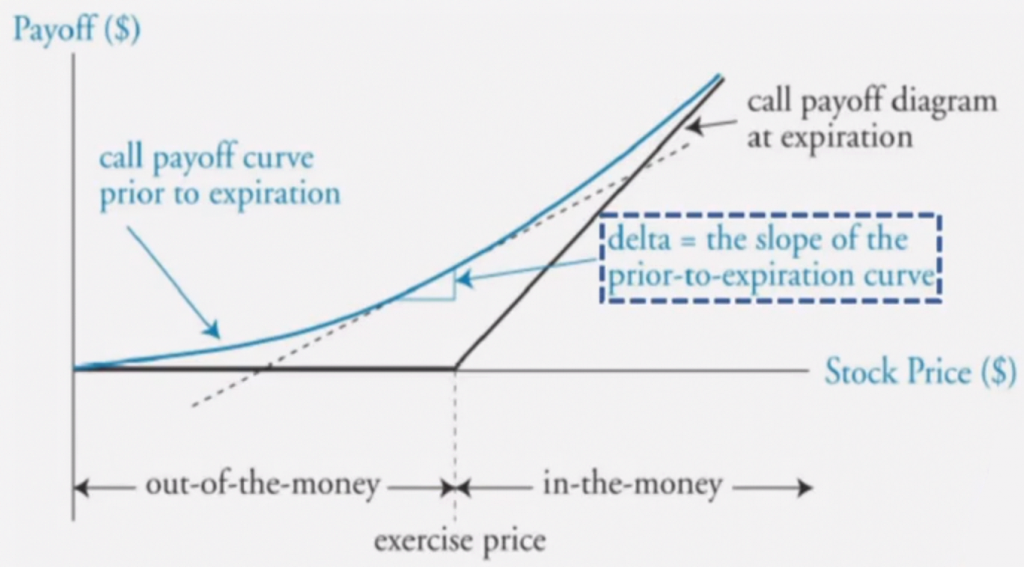
因此不难推出 call 和 put 的 Delta 取值范围:
$$ 0 \leq Delta_{call} \leq 1$$
$$ – 1 \leq Delta_{put} \leq 0 $$
\( Delta_{call} \) 与 \( Delta_{put} \) 的关系
对于无股利支付的 call & put,满足下面两个式子:
$$ Delta_{call} = N(d1) $$
$$ Delta_{put} = – N(- d1) = N(d1) – 1 $$
由此我们可以得到 call & put 的 Delta 值的重要关系:
$$ Delta_{call} – Delta_{put} = 1 $$
其实这个关系可以通过 买卖权平价公式很容易得到:
由:
$$ C_{0} – P_{0} = F_{0}(T) $$
等式左右两边同时对股价 S 求导,即可得到:
$$ Delta_{call} – Delta_{put} = 1 $$
Delta 随 S 变动图像
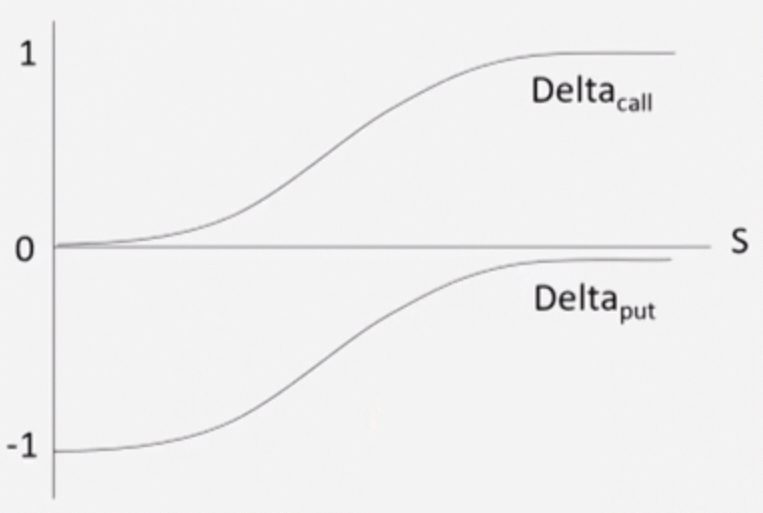
tips:当股价 S 等于行权价 K 的时候,\(Delta_{call}\) 值刚好等于 0.5, \(Delta_{put}\) 刚好等于 – 0.5 。
这里不给证明过程
如果 Delta 的绝对值在 0 – 0.5 之间,说明是一个价外期权(OTM)。
如果 Delta 的绝对值在 0.5 – 1 之间,说明是一个价内期权(ITM)。
time passage 带来 Delta 变动的图像
随着期权临近到期,时间价值(TV)就越小,option price 就会逐渐向内在价值(IV)贴近,\(|Delta_{otm}|\) 就会逐渐向 0 贴近, \(|Delta_{itm}|\) 就会逐渐向 1 贴近。
因此可以得到下图:
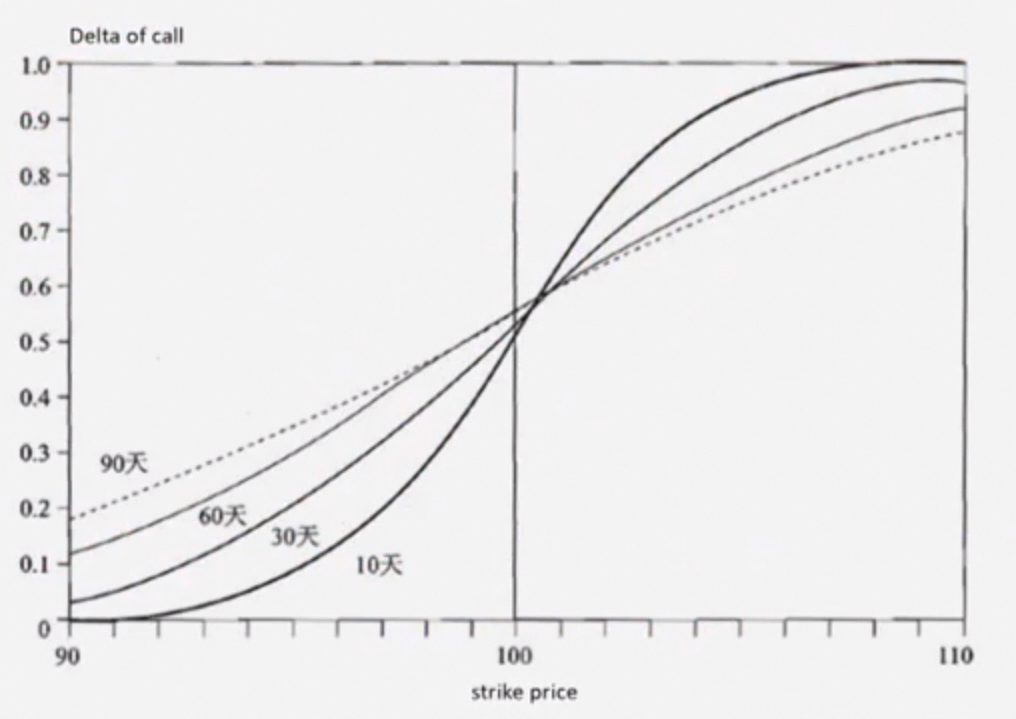
Delta 对冲
如果我们有着如下对冲组合:由 Delta 份 ETF 空头和 1 份 ETF 看跌期权空头组成(或者由 Delta 份 ETF 多头和 1 份 ETF 看涨期权空头)。当 ETF 价格变化 0.001 元时,Delta 份 ETF 空头价格会变化 -0.001 * Delta 元,1 份ETF 期权合约价格会变化 0.001 * Delta 元。两者相互抵消,对冲组合的整体价格几乎不变。因此,我们可以用 Delta 份 ETF 空头去对冲 1 份看跌期权多头。
注意:在 delta 对冲中,期权的份数一定是比 ETF(正股)数量要多的。
Delta 对冲是一个动态调整的过程,随着股价 S 的变化和时间的推移,Delta 会随之变动,也就是说,我们的 portfolio 的对冲比率要动态调整。
计算杠杆
比如ETF上涨1%,期权上涨10%,那么期权的杠杆就是10倍。那么通过Delta,我们可以计算期权的杠杆倍数。
假设目前 ETF 的价格是 3.00 元,有一份 1 个月后到期行权价为 3.20 的 Call,现在的价格是 0.10 元,Delta 为 0.33。如果 ETF 上涨 1%,也就是 0.03 元,期权价格就会上涨 0.030*Delta,等于 0.01 元。从涨幅来看,期权合约上涨了 10%。因此,期权合约的杠杆大概是 10 倍。
Gamma 值
Gamma 就是 Delta 随标的价格变化而变化的敏感度。当 ETF 价格变化 0.001 元时,Delta变化 0.001*Gamma。
Gamma 反映的是资产价格变化引起 Delta 的变化,Gamma 越大,代表 Delta 对标的资产价格越敏感,你的头寸的变化,调整的压力就越大。
因此,Gamma 表示的是对冲风险的难度。一般我们希望 Gamma 小一些。
看涨期权和看跌期权有相同的 Gamma。
Long position (call / put) 的 Gamma 是正数。
Short position (call / put) 的 Gamma 是负数。
Gamma 随 S 变动图像
下图是以 long position 为例,Gamma 随 Stock Price 的变化图。
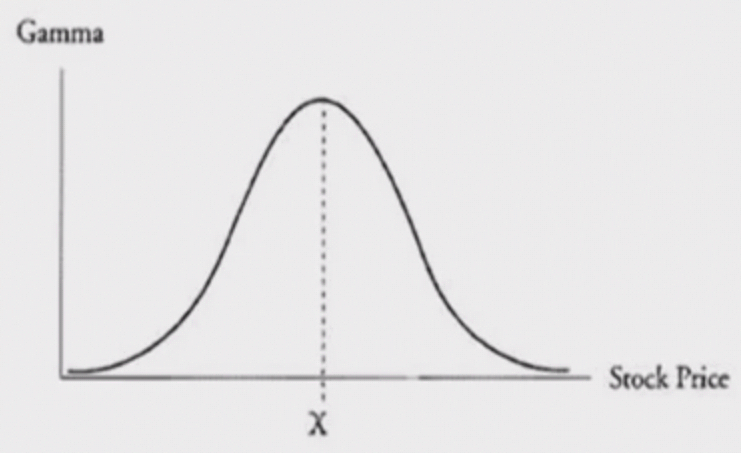
Gamma 在 at-the-money 的时候绝对值达到最大,而在 deep-in-the-money 和 deep-out-of-money 的时候趋近于 0。
time passage 带来 Gamma 变动的图像
随着到期日临近,Gamma 如何变化呢?
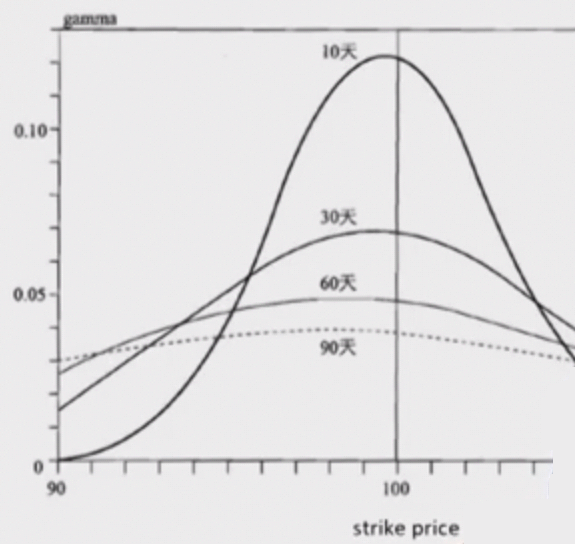
如果股价在执行价附近,随着到期日临近,Gamma 变大。
但是如果是 deep-in-the-money 和 deep-out-of-money 的期权,Gamma 是在逐渐靠近 0 的。
Gamma 对冲
假设对冲组合由 Delta 份 ETF 空头和 1 份期权多头组成,Delta 会随着 ETF 价格变化而变化。当 ETF 价格发生变化时,为了保证对冲的效果,需要调整 ETF 的头寸 Delta。当 ETF 价格变化 0.001 元时,ETF 的头寸 Delta 也会相应的变化 0.001*Gamma。
期权是既带 Delta,又带 Gamma 的。而股票是只带 Delta(等于 1),不带 Gamma 的。
所以,在构造 Gamma-Neutral Position 的时候,要先用 call 和 put 把 Gamma 对冲掉,然后再通过加 long/short stock 的方式把 Delta 对冲掉。
Gamma risk
BSM Model 假定股票价格是连续变动的,不存在跳空缺口,但是现实中股票是会出现跳空缺口的。持有一个 delta-neutral portfolio 就会存在 Gamma 风险。
如果 BSM model 的假设(股价连续变动)成立,就不存在 Gamma 风险。
Theta 值
Theta 衡量的是期权时间价值的损耗,对期权的买方,Theta 一般为负数,用来提醒期权买方,时间是敌人。随着到期日的临近,在其他条件不变的情况下,期权的时间价值会降低。相应地,期权的卖方的 Theta 为正数,意味着时间的流逝对你有利。
$$ Theta = \frac{\Delta C}{\Delta t} $$
此处时间不是指距离到期日时间的长短,而是已经流逝的部分(time passage)。
随着时间流逝,大多数的 call 和 put 的价值都是在减少的,所以无论是 call 还是 put, Theta 通常都是负的。
但是!deep-in-the-money Put 的 Theta 是正的,原因就在于标的的下跌是有限的。
Theta 图像
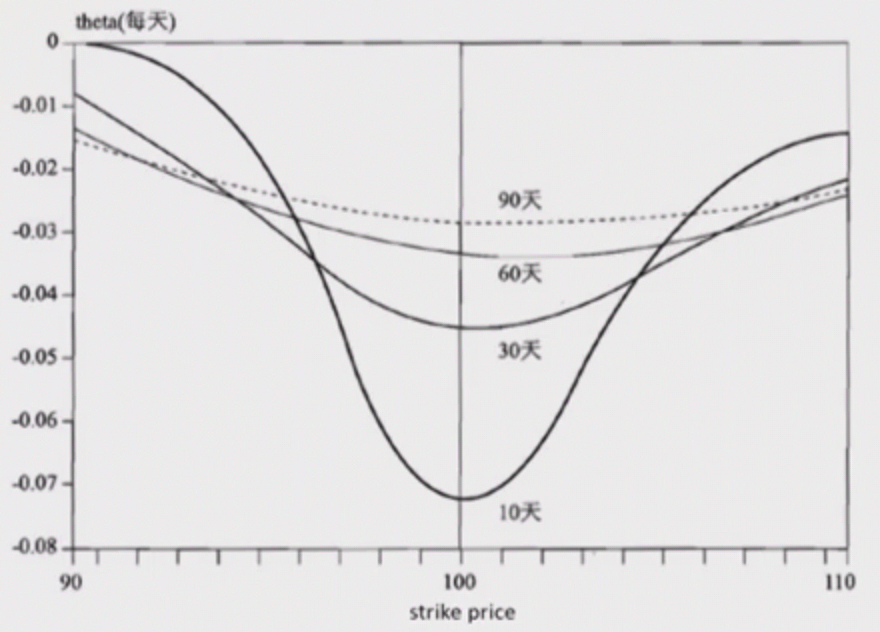
如果股价在执行价附近,随着到期日临近,Theta 的绝对值是在变大的,价值在加速消耗。
但是如果是 deep-in-the-money 和 deep-out-of-money 的期权,Theta 是在逐渐靠近 0 的。
tips:Gamma 和 Theta 图像呈现一个镜像的关系哦。
Vega 值
通常,不确定性越大,风险也就越高,承担风险的一方自然要求更高的补偿。在期权的世界里,预期波动率描述了人们对未来的不确定程度。类似于保费,对于预期波动比较大的资产所对应的期权,期权卖方也会收取更高的期权费。
Vega 是用来衡量期权价格和预期波动率之间的关系。
其他因素不变,期权价格随着标的资产预期波动率的增加而上升,因此不论 Call 还是 Put ,Vega 都是大于零的。
当股票价格在行权价附近的时候,Vega 值会更大一些。
随着到期日临近,Vega 是逐渐变小的。
Rho 值
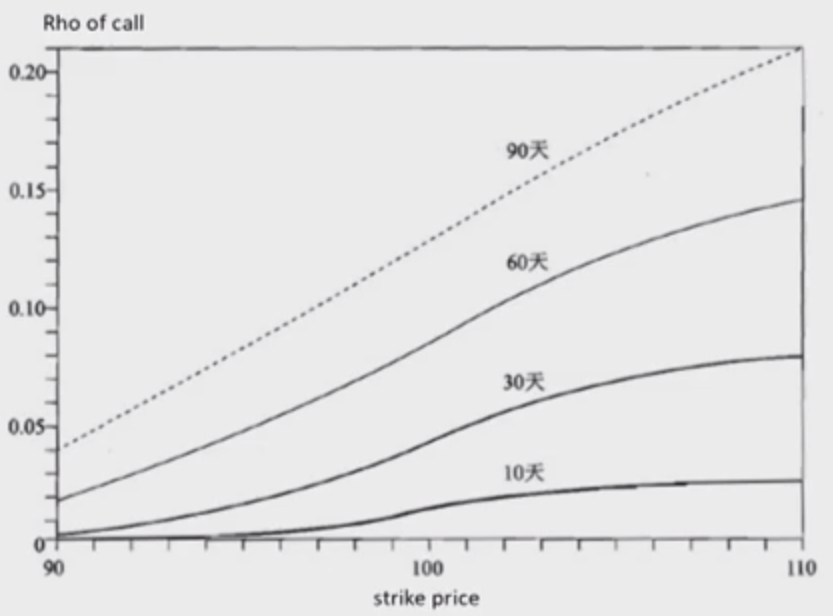
Rho 是指期权价格对无风险利率变化的敏感程度,代表着利率每改变 1%,期权将会出现的变化。标的资产价格越高,距离到期日时间越长,Rho 就越大。
看涨期权的 Rho 为正,看跌期权的 Rho 为负。
Rho 相较于其他希腊值字母,对于期权的影响是最小的。
如果你想了解关于什么是期权以及如何利用期权组合设计策略,请点击:
发表评论