本文源自SpindleHdeging股指对冲策略的引申思考，请先阅读原帖再来阅读本文。

由于标的最小步长带来的向量角度误差

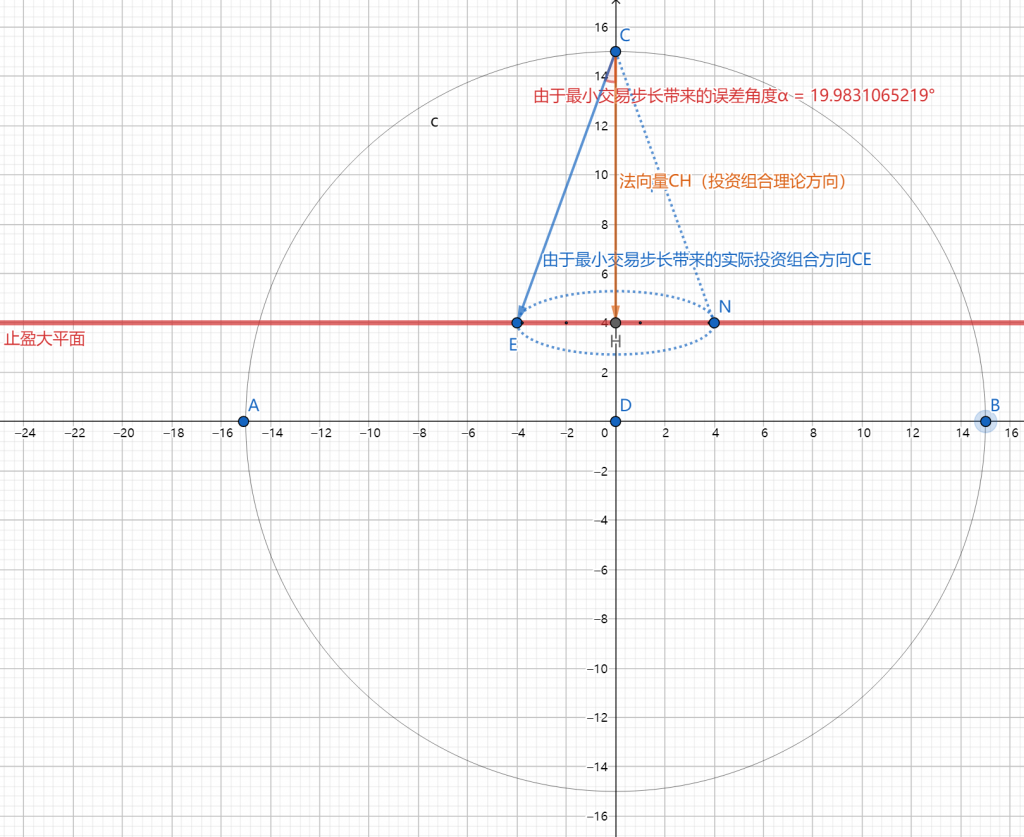
为什么会存在误差角度？

如图所示，理论上我们在C点建立的投资组合，方向应该是CH方向（止盈大平面的法向量）。但是由于经纪商有最小交易步长限制，导致我们不能随心所欲配置自己头寸的数量，而是有最小配置单位（例如0.01手）。这样就出现了，我们不得不对自己每个标的的手数进行圆整，圆整到经纪商允许的手数（例如将0.017手圆整成0.01手或者0.02手）。圆整之后的投资组合方向假定是CE方向，CE和CH之间的夹角就是由于最小交易步长带来的误差角度α。这也就是为什么我们会限定策略允许运行的最小资金量。这其实是受到了经纪商标的的局限，而非我们自己杜撰。只有限定了最小资金量，这一误差才可以小到可以忽略，不至于对策略运行影响过大。

如何确定每个平台对应的最小资金量，以及对应的误差角度？

那么根据每个平台的德指、日经、恒指的规格，如何确定对应的最小资金量，以及对应的误差角度呢？这里其实常规的做法是把理论法向量CH的方向，和实际投资组合方向CE两个向量求夹角。但是由于三个标的的计价货币不同（分别是欧元、日元和港币），为了保证各个方向的残差运动反映到账户上的盈亏是统一的，我们在做模型的时候，会把三个方向的头寸进行一个标准化。标准化之后的单位残差对应的计价货币就统一成了美元。但是这里有一个难点，在于如何保证自己选的位置就是误差角度最大的位置呢？这个问题虽然也能做，但是有点烧脑。因此我们没有选用最常规的做法，而是用蒙特卡洛实验来完成同样的效果。

蒙特卡洛实验

常规的解法需要找到误差角度最大的位置对应的德指、日经和恒指的报价。但是我们用计算机循环的方法，把前两个标的的价格取随机数来计算第三个价格（法向量与止盈平面垂直）。得到的结果对应的为最大误差角度，经过上千次循环之后，把最大的误差角度记录下来，尽管这不一定对应的是最大误差角度所对应的位置，但是数值会随着循环次数的增加而不断逼近理论值，反正计算机又不累。

附上python代码：

import numpy as np


class Coordinate:
    def __init__(self, x, y, z):
        self.x_axis = float(x)
        self.y_axis = float(y)
        self.z_axis = float(z)

    def show_axis(self):
        print("x_axis = ", self.x_axis, ", y_axis = ", self.y_axis, ", z_axis = ", self.z_axis)


def dot_product(vec1, vec2):
    return vec1.x_axis*vec2.x_axis+vec1.y_axis*vec2.y_axis+vec1.z_axis*vec2.z_axis


def norm(vector):
    return np.sqrt(vector.x_axis**2 + vector.y_axis**2 + vector.z_axis**2)


def flots(lots, minlots):
    stepnum = 0
    if lots < 0.5*minlots:
        return 0
    elif lots < minlots:
        return minlots
    else:
        stepnum = int(np.round((lots - minlots)/minlots))
    return minlots + stepnum * minlots
ax, ay, az = 18887, 15642, 9560.9
bx, by, bz = 31977, 24008, 13390
normalvector = Coordinate(ax-bx, ay-by, az-bz)


"""-----------------------------------------
下面根据平台规格设置参数
-----------------------------------------"""
# 设置最小手数
minlotsDE, minlotsHK, minlotsJP = 0.01, 0.01, 0.01
# 残差敏感度
sensitive = 1
# 小数点位
digitsDE, digitsHK, digitsJP = 0.1, 0.01, 0.1
# 汇率
xrateEUR, xrateHKD, xrateJPY = 1.1, 1/7.8486, 1/108
# 合约大小
contractDE, contractHK, contractJP = 25, 50, 500
# 复利乘数
compound = 1
# 计算点值
tickvalueDE = digitsDE * xrateEUR * contractDE
tickvalueHK = digitsHK * xrateHKD * contractHK
tickvalueJP = digitsJP * xrateJPY * contractJP
print("tickvalue of DE = ", tickvalueDE)
print("tickvalue of HK = ", tickvalueHK)
print("tickvalue of JP = ", tickvalueJP)


"""-----------------------------------------
循环蒙特卡罗
-----------------------------------------"""
max_angel = 0
for i in range(1000):
    # choose random vector that is vertical with normal vector
    randx = np.random.uniform(-1, 1, 1)[0]
    randy = np.random.uniform(-1, 1, 1)[0]
    randz = -(randx * normalvector.x_axis + randy * normalvector.y_axis) / normalvector.z_axis
    standard = np.sqrt(randx**2 + randy**2 + randz**2)
    randx /= standard
    randy /= standard
    randz /= standard
    randvector = Coordinate(abs(randx), abs(randy), abs(randz))
    # calculate neariest lots vector
    lots1 = flots(sensitive * abs(randx) * digitsDE / tickvalueDE, minlotsDE)
    lots2 = flots(sensitive * abs(randy) * digitsHK / tickvalueHK, minlotsHK)
    lots3 = flots(sensitive * abs(randz) * digitsJP / tickvalueJP, minlotsJP)
    lots1 *= (tickvalueDE/digitsDE/sensitive)
    lots2 *= (tickvalueHK/digitsHK/sensitive)
    lots3 *= (tickvalueJP/digitsJP/sensitive)
    lotvector = Coordinate(lots1, lots2, lots3)
    # randvector.show_axis()
    # lotvector.show_axis()
    # print("----------------------------------------")
    # calculate the angel of lots vector and random vector
    costhetha = dot_product(randvector, lotvector)/(norm(randvector)*norm(lotvector))
    angel = np.arccos(costhetha)
    # update the largest angel
    max_angel = max(angel, max_angel)

# print the largest angel
print("max angel = ", max_angel/np.pi*180)

顺便贴上蒙特卡洛的维基百科：

蒙特卡罗方法（英語：Monte Carlo method），也称统计模拟方法，是1940年代中期由于科学技术的发展和电子计算机的发明，而提出的一种以概率统计理论为指导的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。

20世纪40年代，在科學家冯·诺伊曼（John von Neumann）、斯塔尼斯拉夫·烏拉姆（Stanisław Marcin Ulam）和尼古拉斯·梅特罗波利斯（Nicholas Constantine Metropolis）於洛斯阿拉莫斯国家实验室为核武器计划工作时，发明了蒙特卡罗方法。因为烏拉姆的叔叔经常在摩納哥的蒙特卡洛赌场输钱得名，而蒙特卡罗方法正是以概率为基础的方法。与它对应的是确定性算法。

最佳的调仓时机

以下用“调仓”代表仅对投资组合进行角度的调整，而非加仓或者减仓。

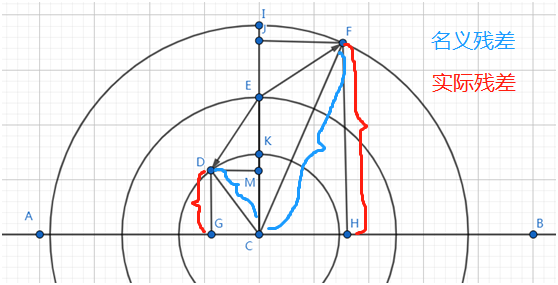
由之前的文章我们看到，我们这一模型的优势W=KM=EM-EK。

EM可以定义为实际价格向止盈平面运动的距离。

EK可以定义为实际价格向圆心运动的距离。

于是我们就把优势W分解为一个沿止盈平面的运动和一个沿圆心方向的运动。

如果希望优势W达到最大，就是希望二者的差尽可能拉大。也就是说，当实际价格沿圆心的运动距离EK不动，而沿止盈平面运动的距离尽可能大的时候，W达到最大。

我们发现，角度变化较小的话，如果调仓频率过高，会破坏我们已有的优势，导致实际残差相对于名义残差的优势较小，所以我们不会设置一直去调整到最优角度。但是当角度偏移较大的情况下，调仓显然比不调仓更有优势。

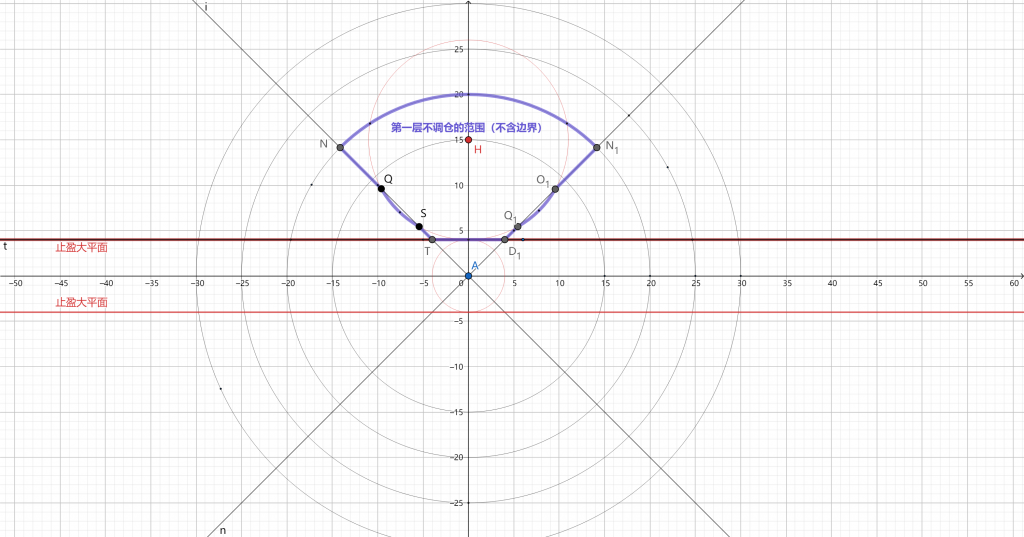
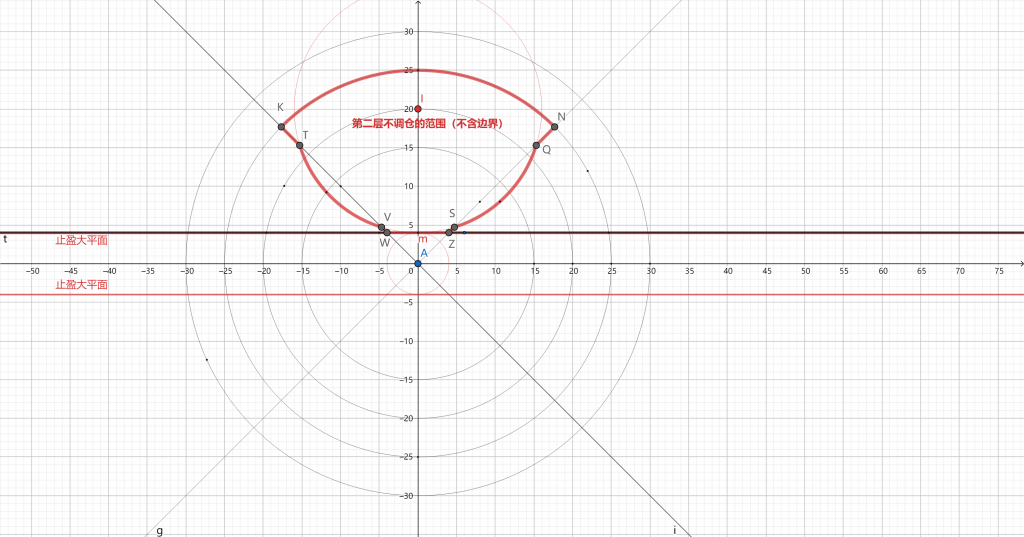
为了保证角度偏移足够大才调仓，我们把45°作为分界线，偏移不足45°的我们完全不调仓，偏移超出之后的优势已经比较明显，我们才考虑是否调仓。

我们假设H点进场之后，随机游走是以H点为中心向外辐射的，那么同一圆上的落点概率相同。s点是沿最近方向打到止盈点的位置，那么到达Q点、S点、Q1点、O1点的概率和s点的概率相同，结果却出现一个止盈了，一个还在游走。所以我们以进场点H为圆心，以Hs长度为半径做一个圆。当组合价格偏移到圆外并且在45°直线外的情况下我们选择调仓，图形如下，每一层左右是对称的，图中只画了单侧。

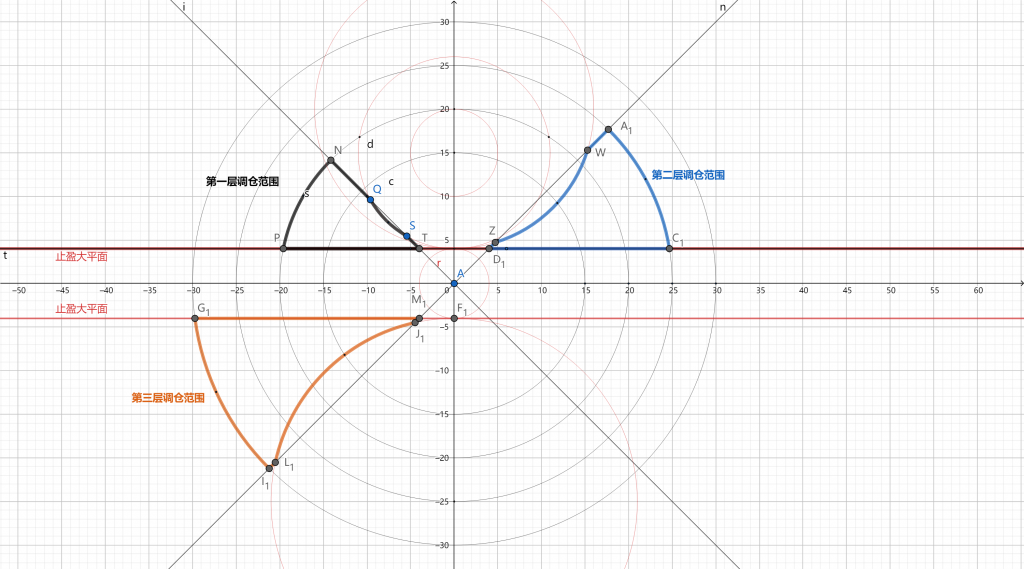
在新版本中，我们把调仓区域按照上图进行了调整，回测结果点击这里

MT4下载地址：SpindleHedging(MT4)

MT5下载地址：SpindleHedging (MT5)