在上一篇《二叉树期权定价模型(一)》里面,我们主要介绍的是二叉树基本的建模和一个分叉阶段的二叉树。这一篇将要介绍一下在无套利下的两个分叉阶段的二叉树模型下,如何计算欧式期权和美式期权的价值。
Two-Period Binomial Model for European Option
Two-Period 代表的是从 0 时刻到期权到期是时刻,总共分叉两次,如下图所示。
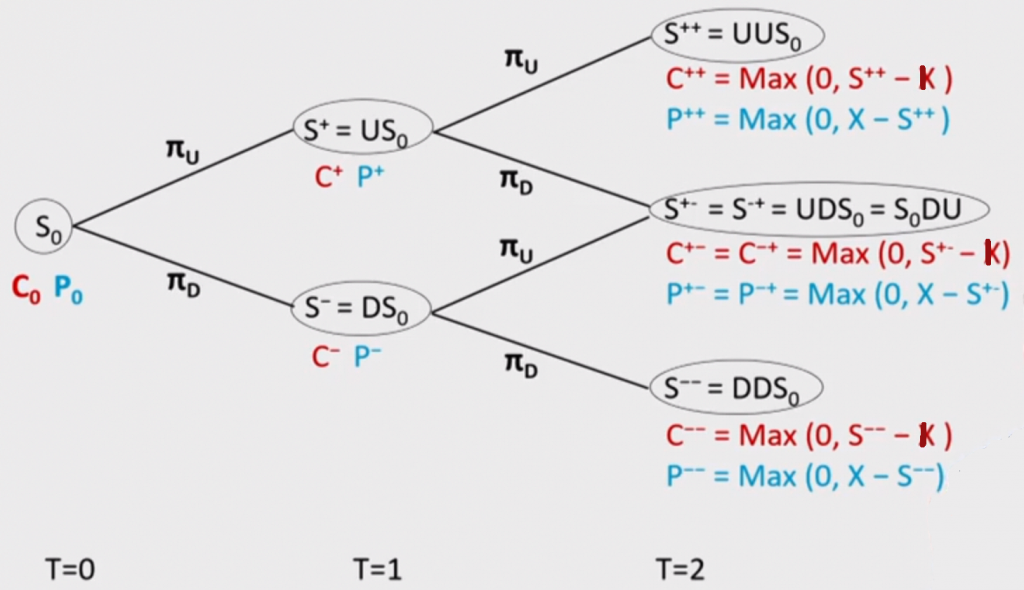
欧式期权的二叉树定价模型计算步骤
- 先通过 U 和 D 和 Risk-free-rate 把风险中性下的上涨下跌概率算出来\(\pi_{U}\) 和 \(\pi_{D}\)
- 进而算出股价二叉树每一阶段的股价
- 从期权到期日(最后一个分叉的节点)计算 call 和 put 的价值(也即内在价值,也即 payoff)
- 从后向前,用分叉后的两个节点的 call 和 put 的价值以及 \(\pi_{U}\) 和 \(\pi_{D}\),以及 Risk-free-rate 和每个分叉阶段的时间(折现用) ,去推算前一个分叉点的 call 和 put 的价值
- 重复第 4 步直到推算到起始的 call 和 put 的价值
Two-Period Binomial Model for American Option
在研究美式期权二叉树之前,我们要先来回顾一下美式期权提前行权的内容。
美式期权提前行权
无股利支付的 American call 是不应该提前行权的,因为持有 call 的价值是大于提前行权的拿到的价值的,理性的投资者不会这么做。
有股利支付的 American call 是有可能提前行权的,具体看分红是否足够诱人。
深度实值的 American put 也是有可能被提前行权的。
详细的关于美式期权是否应该提前行权的原因,请参考:
两个阶段的美式期权二叉树模型
对于可能被提前行权的美式期权(也就是说,无股利支付的 American call 是不需要进行如下判断的,直接当成 European call 即可),我们需要对每个节点判断一下是否会提前行权。
- 如果一个节点,提前行权的价值的大于无套利下计算的价值,就应该选择提前行权。
- 每个节点的价值取 max {exercise value,calculated price}
注意:
- CFA 考试中如果只分叉两次,只能在节点的时间点行权,其他时间点是不能行权的,所以不是标准的美式期权。留意题目中说的行权可以在哪里实施,以题目为准。
- 0 时刻的节点也是可能允许行权的,如果通过二叉树从后往前退出来的 0 时刻的 calculated value 比 0 时刻直接行权价值还小,那么应该选择 0 时刻直接行权。
美式期权的二叉树定价模型计算步骤
- 先通过 U 和 D 和 Risk-free-rate 把风险中性下的上涨下跌概率算出来\(\pi_{U}\) 和 \(\pi_{D}\)
- 进而算出股价二叉树每一阶段的股价
- 从期权到期日(最后一个分叉的节点)计算 call 和 put 的价值(也即内在价值,也即 payoff )
- 从后向前,用分叉后的两个节点的 call 和 put 的价值以及 \(\pi_{U}\) 和 \(\pi_{D}\),以及 Risk-free-rate 和每个分叉阶段的时间(折现用) ,去推算前一个分叉点的 call 和 put 的价值 (calculated value)
- 对第 4 步计算的 calculated value,和当前节点直接行权的 exercise value 进行比较大小,取 max {exercise value,calculated value} 作为当前节点的 call/put 的价值
- 重复第 4 -5 步直到推算到起始节点的 call 和 put 的价值 calculated value 。同样把起始节点的 calculated value 和直接行权的价值比较大小,取 max {exercise value,calculated value}

分享到
发表评论