Interest Rate Risk 利率风险
Reinvestment Risk 再投资风险
对于plain vanilla bond 的投资者,会面临 coupon payment 的再投资风险。
利率下行,投资者会更担心再投资风险。
Market Price Risk 市场价格风险
如果债券投资者不打算持有到到期,而是打算提前卖掉,就会面临市场价格风险。
利率上行,投资者会更担心市场价格风险。
Reinvestment Risk & Market Price Risk
由上可见,Reinvestment Risk 和 Market Price Risk 随利率是反向变动的,具体要看哪个占主导,更 care 哪个风险。
如果债券的投资期限比较短,再投资风险比较小,市场价格风险就比较大。市场价格风险占主导,意味着投资收益和利率呈反向关系。
如果债券的投资期限比较长,再投资风险就比较大(中间的每一笔 coupon 都需要面临),市场价格风险就比较小(临近到期,债券价格炒作空间小波动小)。再投资风险占主导,意味着投资收益和利率呈正向关系。
那么,如何定义债券的投资期限是长还是短呢,就要进入麦考利久期的概念。
Macaulay Duration 麦考利久期
Modified Duration 修正久期
Properties of Duration 久期的性质
当其他因素一致的情况下:
1 . time-to-maturity 越长,久期越大
2 . coupon rate 越大,久期越小
3 . YTM 越大,久期越小
CFA考试中记住上面三条性质即可,但是实际的久期图如下图,了解即可。
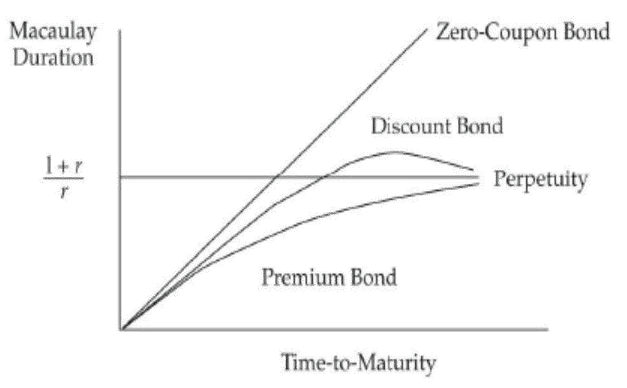
Term Structure of Yield Volatility 收益率波动率的期限结构
长端利率的波动率是比较小的,短端利率的波动率是比较大的。这导致收益率波动率的期限结构是斜向下的。
债券价格变化是如下两个因素共同作用的:
- YTM 的变动带来的影响(久期的变动)
- YTM变动的基点数
短期债券的价格波动率,有可能比长期债券更大,主要是因为收益率波动率大占主导。
Bond Portfolio Duration 债券投资组合的久期
债券投资组合的久期就等于每个债券久期的加权平均。
$$Portfolio duration = w_{1}D_{1}+ w_{2}D_{2}+…… w_{n}D_{n}$$
其中,
$$ w_{1}+ w_{2}+…… w_{n}=1 $$
上式成立有一个前提条件,就是收益率曲线发生的是 parallel shift(平行移动)。
Dollar Duration 美元久期
Dollar Duration,也叫 Money Duration,代表利率变动 1%,债券价格变动多少元。
$$ Dollar Duration = \frac{\Delta P}{\Delta r} $$
Dollar Duration,在价格-收益率曲线上代表曲线切线的斜率。
由定义式可以看出,美元久期和修正久期的关系:
$$Dollar Duration = Modified Duration \times P $$
投资组合的 Dollar Duration,等于每一个单一债券的 Dollar Duration 直接相加,不需要加权平均。
Price Value of Basis Point 基点价格值(PVBP)
PVBP 是指,当利率变动 1 个基点的时候,债券价格变动多少元。
根据定义,PVBP 就是美元久期的百分之一。
CFA 考试中如果让计算 PVBP,就用如下公式
$$PVBP = \frac{P_{-} – P_{+} }{2} $$
Effective Duration 有效久期
Macaulay Duration 和 Modified Duration 面对含权债券是不适用的,因此要引入 Effective Duration。
为什么 Macaulay Duration 和 Modified Duration 面对含权债券不适用?
Macaulay Duration 是用来衡量未来现金流的平均回流时间。
callable/putable bond,最大的问题是时间长短不确定(callable bond 投资者不确定发行方什么时候行权,putable bond 投资者也不知道自己未来什么时候行权,因为未来的利率路径不确定),无法用 Macaulay Duration 进行测度。
Modified Duration 衡量的是利率(YTM)变动 1%,债券价格变动百分之几。
callable/putable bond 本身不能保证会持有到期,所以 YTM 没有意义,我们转向用的是 YTC 和 YTP 来衡量持有到行权的收益率。
由于未来的利率变动路径是不确定的,不同期限的利率点都可能影响是否行权。所以单一利率点的变动,对于含权债券的久期是不确定的,但是,如果整条利率曲线是平行移动的,含权债券什么时间行权是最佳时点就确定了,那么就可以衡量它的久期了。
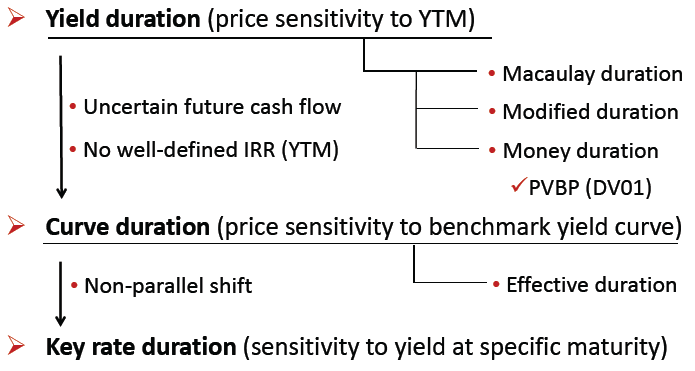
Yield Duration & Curve Duration 收益率久期 & 收益率曲线久期
前文讲过的 Macaulay Duration 和 Modified Duration 都属于 Yield duration 收益率久期,衡量的是单一利率点的变动对债券久期的影响。
Effective Duration 则是属于 Curve Duration,衡量的是整条 benchmark yield curve(基准收益率曲线)发生 parallel shift(平行移动)带来的债券价格变动的敏感程度。
$$EffDur = \frac{P_{-} – P_{+} }{2 \times \Delta curve \times P_{0}} $$
Tips:有效久期不是只能研究含权债券。普通的不含权的债券,也可以用有效久期来衡量,假定整条利率曲线发生 parallel shift 平行移动来进行研究。
Key Rate Duration 关键利率久期
实际在研究 Effective Duration 的时候,如果利率曲线发生 parallel shift 当然是最好的。但是如果是 nonparallel shift 非平行移动,其实几个关键的发生现金流的利率点的利率发生平行移动,一样可以使用 Key Rate Duration 来衡量债券的久期。
发表评论