Pricing Bond with a Single Discount Rate 单一折现率为债券定价
Bond Value 就是未来现金流的现值。
首先我们回顾一下DCF模型的公式:
$$V_{0} = \sum_{i=1}^{+\infty} \frac{CF_{i}}{(1+r)^{i}}$$
如果市场是公允的没有套利机会的,市场价格应该等于其内在价值的。那么在单一折现率下,普通香草型债券价值的公式:
$$P_{0} = V_{0} = \sum_{i=1}^{n} \frac{C_{i}}{(1+r)^{i}} + \frac{Par}{(1+r)^{n}}$$
其中,
- \( C_{i} \)是每一期的 Coupon
- Par 是到期偿还的本金
- r 是折现率
Spot Rates 即期利率
关于什么是即期利率,即期利率和远期利率什么区别,我们在之前远期利率协议的文章中讲过。
即期利率,也是未来一笔单一现金流(例如零息债券)的折现率。因此 Spot rates 也被叫做 zero rates。
Spot rates 反映了 zero-coupon bonds 的到期收益率。
有了这个概念,我们也就得到了 Bootstrapping (剥息法)给普通香草型债券定价的方法。我们把原来每一期的 Coupon值 \(C_{i}\),当成是一个 i 年期的零息债券,即期利率为 \(r_{i}\),于是有了如下式子:
$$P_{0} = V_{0} = \frac{C_{1}}{(1+r_{1})^{1}} + \frac{C_{2}}{(1+r_{2})^{2}} +…… + \frac{C_{n}+ Par}{(1+r_{n})^{n}}$$
注意,上式是从右向左求解的。已知未来现金流和每一期的即期利率,来求解债券的价值。
以上我们探讨的 Spot Rate,是无信用风险的零息债券,这是一个假定前提。
Spot Rate Curve 即期利率曲线
Spot Rate Curve 是反映一系列即期利率和到期日的关系图。它反映了即期利率的期限结构。
随着时间的推移, Spot Rate Curve 是持续变化的。
Yield Measures 收益率衡量
Forward Rates 远期利率
Forward rate 是在远期市场上交易的 bond 或者 money market instrument 的利率。
举例:2y5y,代表 2 年后开始的 5 年的利率。第一个数字代表远期合同开始的时间。第二个数字代表 tenor(期限)。
Implied forward rates(隐含的远期利率,IFR)

其中,\( IFR_{A,B-A} \) 是A时间点到B时间点这个时间段的远期利率,期限是 (B-A),也可以写成 Ay(B-A)y。
由上式,有了不同期限的即期利率(一条即期利率曲线),就可以计算所有的远期利率。
当 r 趋近于0 时,\( (1+r)^{n} \approx 1+n \times r\)。
上式可以用于在计算远离利率时候的近似估算。
Maturity Structure of Interest Rates 利率的期限结构
Spot curve / zero curve 即期利率曲线
一系列的 zero-coupon bonds 的 YTM。
Forward curve 远期利率曲线
一系列具有相同 tenor (期限)的远期利率绘出的曲线。
注意:曲线上的一系列远期利率的时间段是一样的。例如:my1y,或者 my0.5y。
举例:假设 2y1y = 4%,3y1y = 4.5%,那么对应在 Forward Curve 上的坐标点分别是(3, 4%)和(4, 4.5%)。其中,横坐标是两部分年限相加。
Yield curve
YTMs 和 maturity 之间的关系。
Yield curve 也是可以通过即期利率曲线得到的。
Quote Conventions 报价管理
债券的报价和实际交易的价格会有不同,当中存在一个 Accrued Interest(应计利息)。
Accrued Interest 应计利息
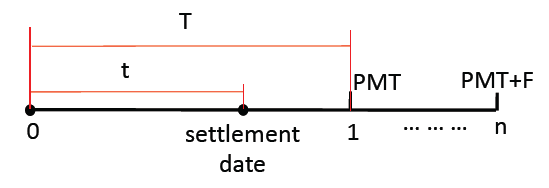
债券的报价是只包含利得,不包含 coupon 的。所以如果债券在两个付息时间点中间进行交易时候,买方需要额外补偿给卖方一部分 Accrued Interest 的,这部分应计利息的计算是要按照持有时间占一个付息周期的比例来计算的。
$$ AI = \frac{t}{T} \times PMT $$
Clean Price / Flat Price
tips:债券的报价报的是 Clean Price / Flat Price。
Dirty Price / Full Price
Full Price = Clean Price + Accrued Interest
tips:债券的成交价格是 Dirty Price。
债券报价用 clean price 有什么好处呢?
- 有利于投资者区分,coupon 和价格炒作两部分带来的债券价格变动。
- 如果报 dirty price,债券的价格就会成现锯齿状,每次付 coupon 的时间点都会不平滑。
计算 Clean Price 和 Dirty Price 的步骤
- 计算交易日之前最近的一个付息日,债券的理论价格(PV)
- 将PV以复利的形式累积到交易日,得到交易日的 full price(\( PV \times (1+r)^{\frac{t}{T}} \))
- 用交易日的 full price,减去单利形式计算的 AI,得到前面最近的一个付息日的 clean price
Matrix Pricing 矩阵定价
估值方法:
- 绝对估值法: 用与自己有关的信息,例如 DCF 模型,用自己未来的现金流向前折现
- 相对估值法:用其他类似的品种的定价来为自己的定价,例如市盈率和市净率,公司行业业务范围相近的公司,用相似的 PE 或 PB 来近似估值
本节要讲的 matric pricing 就是相对估值法。用 maturity 和 coupon rate 和 credit quality 比较相近的一系列交易更活跃的 bonds 的 YTM ,来估算出交易不活跃的或者尚未发行的某只目标 bond 的 YTM 和 price。
Linear interpolation 线性差值法
有了一系列相近的 bonds,我们就会用到 linear interpolation,通常是基于 maturity 进行的,例如要估值的目标 bond 是 3 年期,取的相似债券分别是 2 年期和 5 年期。
这样就可以求出目标 bond 的 YTM,进而也可以求出相对于某个 benchmark 利率的 yield spread。benchmark rate 通常是取到期日相近的国库券的 YTM。
Yield Spread 收益率基差
基差表面上是反映收益率的差,其实是在对风险进行度量。
Nominal Spread 名义基差(点对点的差异)
Yield spread over benchmark 是指目标债券的收益率和 benchmark rates 的差。选择不同 benchmark 就有不同的名字,用的最多的是 G-spread 和 I-spread。
G-spread
Yield spread over gvernment bond
I-spread
Yield spread over the standard swap rate
其中,standard swap rate 是指,在普通香草型的利率互换中,固定端的利率。
由此可见,Norminal Spread 都是一个收益率点对 benchmark 点的差异。
Z-spread(线对线的差异)
Z-spread 也叫 zero volatility spread,它是在无风险的 spot curve 的基础上加的一个固定的基差。
在这里隐含了一个假设:收益率曲线是在无风险的 spot curve 基础上,做了一个向上的 parallel shift(平行移动)。
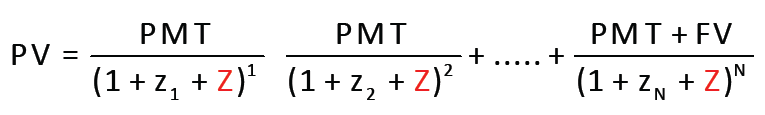
所以,Z-spread 的 benchmark 是无风险的 spot curve,是一条线。
OAS(树对树的差异)
OAS 全称叫 Option-adjusted spread,要解决的是如何去除掉含权债券中的 Option risk 的问题,这样就可以专心研究 credit risk 了。
OAS = Z-spread – Option value(%)
由上式可得:
- Callable bond:option value > 0,OAS < Z-spread
- Putable bond: option value < 0,OAS > Z-spread
对于含权债券,我们的定价一般是构建利率二叉树。那么,OAS就是在利率二叉树的起点,加上一个 credit risk 的补偿值,使得整棵树都向上平移,这个值就是 OAS。
发表评论